ワールド座標変換 World Transform of LocalCoordenate


ワールド座標変換について

前回、ジオメトリックパイプラインの概要を説明しました。
其の時に、ローカル座標系　→　ワールド座標系へ頂点を移動させることを
ワールド座標と言いましたね。

もう一度、確認のために述べます。
ワールド座標変換の目的とは、
ローカル座標系で座標(0,0)を中心として作ったポリゴンを、
様々なポリゴンが存在している、ワールド（グローバル）座標系へと
回転・移動させることです。


頂点座標の行ベクトル・列ベクトル

では、ローカル座標系からワールド座標系へ移動するための、
計算式を見て行きましょう。

３Ｄは三次元でそれぞれＸ（横）、Ｙ（縦）、Ｚ（奥行き）で表されるため、
とある座標があるとすれば、頂点Ａ(432,523,669)等と言った表し方が出来ます。
これを行ベクトルに直すと、
|432,523,669|
列ベクトルだと、
|432|
|523|
|669|
と表すことが出来ます。

前にも述べたとおり、
最終的なベクトル座標の割り出しは、転置マトリックス　×　列ベクトル
で導き出します。
ですので、ここからは列ベクトルとして座標を表すことにします。
|x|
|y|
|z|


座標変換計算において、マトリックスは必須の数学です。
そして、このマトリックスの性質上により、
頂点ベクトルは4要素のベクトルとして扱わなければなりません。
ですので、実際計算する時は、四次元計算になります。

|x|
|y|
|z|
|t|
四番目の要素tは頂点に移動を与えるためのマトリックスを作る時に
関係してくる要素です。
ただ、ベクトル第四要素tは変動させてはいけません。
定数１のまま固定することが条件です。
詳しいことは、後々説明します。



計算順序

マトリックス同士の掛け算は、置換をすると値が変動することは
行列計算の項で述べたと思います。
マトリックス同士の掛け算の順序を間違えると、
変な値になることがあります。
ですので、十分注意しながらプログラムを組んでください。

今からざっと、５つのマトリックスを掛けますが、
これにも順序があり、順番を間違えると結果の値が違います。

Ｘ軸回転マトリックス
Ｙ軸回転マトリックス
Ｚ軸回転マトリックス
移動量マトリックス
スケーリングマトリックス

これを掛け合わせる順序は、



スケーリングマトリックス
×
Ｙ軸回転マトリックス
×
Ｘ軸回転マトリックス
×
Ｚ軸回転マトリックス
×
移動量マトリックス



ここで注目して欲しいのが、
Ｙ軸回転マトリックスが一番先頭に来ていることです。
深くは考えなくて良いので、Ｙ　Ｘ　Ｚと掛け合わせることと
覚えておけばＯＫです。

注意しなければならないのは、
移動量マトリックスを回転マトリックスの前にしないことです。
重心が0,0で回転するので、
移動して、回転させるとポリゴンが思った位置に来てくれません。
下の図を見てください。
置換した掛け算が成り立たないのがわかります。





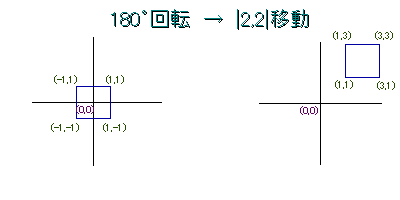
このように、結果が違うので掛け算は
Ｙ軸回転・Ｘ軸回転・Ｚ軸回転・移動量
これより置換を行わないでください。
例外的にスケーリング処理については何処に入れても一緒です。



回転マトリックスの生成

実際にＹ，Ｘ，Ｚについての回転マトリックスを作って見ましょう。


θは回転角を表しています。

Ｙ軸回転マトリックス

	|	 cosθ,	0,	-sinθ,	0|	Ｘ軸についての移動量
	|	    0,	1,	    0,	0|	Ｙ軸についての移動量
	|	 sinθ,	0,	 cosθ,	0|	Ｚ軸についての移動量
	|	    0,	0,	    0,	1|	頂点の相対移動量

Ｘ軸回転マトリックス

	|	1,	    0,	   0,	0|	Ｘ軸についての移動量
	|	0,	 cosθ,	sinθ,	0|	Ｙ軸についての移動量
	|	0,	-sinθ,	cosθ,	0|	Ｚ軸についての移動量
	|	0,	    0,	   0,	1|	頂点の相対移動量

Ｚ軸回転マトリックス

	|	 cosθ,	sinθ,	0,	0|	Ｙ軸についての移動量
	|	-sinθ,	cosθ,	0,	0|	Ｘ軸についての移動量
	|	    0,	   0,	1,	0|	Ｚ軸についての移動量
	|	    0,	   0,	0,	1|	頂点の相対移動量

これらを見ると、
Ｙ軸回転の場合、Ｙ要素だけが変化しません。
Ｘ軸の場合も同様Ｘ要素が固定して、他の要素に変化を与えてます。
ただし、第四要素だけは影響を及ぼしません。


移動マトリックスの生成

移動マトリックス

	|	    1,	   0,	0,	0|	Ｙ軸についての移動量
	|	    0,	   1,	0,	0|	Ｘ軸についての移動量
	|	    0,	   0,	1,	0|	Ｚ軸についての移動量
	|	    Tx,	   Ty,	Tz,	1|	頂点の相対移動量

これは、回転し終わったポリゴンをワールド座標系の何処に配置するか
という移動用マトリックスです。
例えば、(15067,15533,59933)に配置したい場合以下のようにマトリックスを
生成します。

	|	    1,	   0, 	 0,	0|	Ｙ軸についての移動量
	|	    0,	   1,	 0,	0|	Ｘ軸についての移動量
	|	    0,	   0,	 1,	0|	Ｚ軸についての移動量
	|	15067,  15533, 59933,	1|	頂点の相対移動量

四次元でマトリックスやベクトルを扱う理由はここです。
移動の時に四次元マトリックスを使うため、
四次元で処理するのです。


以上のマトリックスを生成したら、
全て掛け合わせ、
最後に出来たマトリックスを転置マトリックスにして、
列ベクトルと掛け算をします。
これでワールド座標変換の計算は終了です。

ワールド座標変換については以上です。