クラメル公式
2005/10/09
クラメル公式は行列で表された連立方程式の解を示す公式だ。2元、3元の場合は以下のようになる。
- a11x+a12y=b1
- a21x+a22y=b2
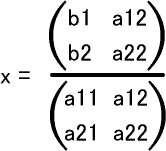
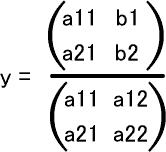
- a11x+a12y+a13z=b1
- a21x+a22y+a23z=b2
- a31x+a32y+a33z=b3
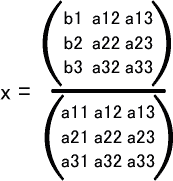
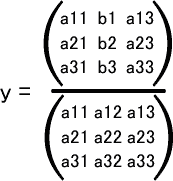
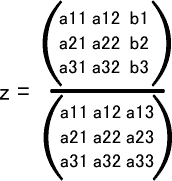
行列式だと連立方程式の解を簡単に表すことができる。
JavaScriptで連立方程式の解を自動生成
2005/10/09
あくまでプログラム重視なので行列の詳しい解説は省く。単に解だけが欲しいならページの一番下を参照してください。
前回のプログラムは、手元で計算した解をプログラムに実装する静止的なものであったが、今回n元連立1次方程式の行列をプログラム自身が解いて答えを求める。プログラムの流れは次のようになる。
最も重要なアルゴリズムは行列の展開にある。一般にn元連立1次方程式の場合、解の項数はn!で示される。nの値し対しての項数は以下のとおり。
| n | 項数 | 変数の使用回数 |
|---|---|---|
| 2 | 2 | 4 |
| 3 | 6 | 18 |
| 4 | 24 | 96 |
| 5 | 120 | 600 |
| 6 | 720 | 4320 |
| 7 | 5040 | 35280 |
| 8 | 40320 | 322560 |
| 9 | 362880 | 3265920 |
| 10 | 3628800 | 36288000 |
| 11 | 39916800 | 439084800 |
| 12 | 479001600 | 5748019200 |
| 13 | 6227020800 | 80951270400 |
計算量は階乗的に増加するので、JavaScriptの計算速度ではn=7でさえ厳しいことになる。数字を書いただけでは実感が湧かないのであれば前回手動で計算した4元連立1次方程式の解を見てほしい。24項であれなのだから、120項ある5はもはや想像がつかない世界だろう。ちなみに項数はこうなるが、代入を繰り返す変数の総使用回数はこれのn倍ある。いかに少ないステップで全ての項をコンプリートするかが最終的な計算速度になる。また、n=4の時点で計算式全体の文字数が2300文字以上ある。5元の場合2万字、6元では20万に膨れ上がる。
2005/10/09
クラメル公式は行列で表された連立方程式の解を示す公式だ。2元、3元の場合は以下のようになる。
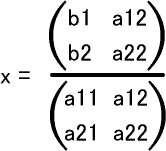
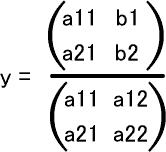
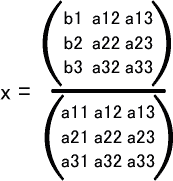
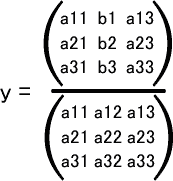
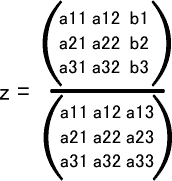
行列式だと連立方程式の解を簡単に表すことができる。
2005/10/09
次はクラメル公式で得られた行列を通常の式に変換する。これに莫大な計算が必要になる。最初に行列式の横列の項の組み合わせを全て洗い出す。2元なら展開すべき列は2つで各列の長さも2なので2回。3元の場合6回、4元では24回。最初の表を見れば分かるが回数は階乗的に増加する。
例えば3元の分母の行列を展開すると次のようになる。
3!個の項ができることになる。ここで例えば何次でもおうようできそうな3次の行列式を展開するJavaScriptを考えてみる。
var r = 3;
document.writeln("<pre>");
for(i=Math.pow(r,r-2);i<Math.pow(r,r);i++){
var str = i.toString(r); if(str.length<r)str = "0"+str;
var ans = 0;
for(j=0;j<r;j++){
if(str.substr(j+1,r-j).match(str.charAt(j)))break;
else ans++;
}
if(ans==r){
for(j=0;j<r-1;j++){
document.write("a",(j+1),(eval(str.charAt(j))+1),"*");
}
document.writeln("a",r,(eval(str.charAt(r-1))+1));
}
}
再帰関数を利用して超高速に求める方法を模索するのは次回にして、とりあえずrに値を代入すると0〜r-1までの数字を組み合わせた全パターンが出力される。n進数を使っているので最大9が限界であるが、そもそもr=7の段階で相当な時間を要するのでn=9なんてJavaScriptでは計算不可能に等しい(r=7のとき5040パターンあるしね)。
ここにr=3を代入すると最初に書いた組み合わせと全く同じものが出力される。
a11*a22*a33 a11*a23*a32 a12*a21*a33 a12*a23*a31 a13*a21*a32 a13*a22*a31
これで1つ目の関門はクリアされた。だがまだ符合が足りない。次は符合を決定する偶順列/奇順列の判別関数を設計する。
偶順列/奇順列とはそれぞれの順列の一番右の添字の数字が1,2,3...と順番になるように並び替える手順数で決まる。例えば、a11*a22*a33は初めから1,2,3が並んでいる。手順は0回で偶数だから偶順列。a11*a23*a32は2番目と3番目を入れ替えて1,2,3になるから手順は1で奇数だから奇順列、という具合だ。つまり、数列をソートするときの移動回数が2で割り切れるかどうかで符合が決定される。
var r = 3;
document.writeln("<pre>");
for(i=Math.pow(r,r-2);i<Math.pow(r,r);i++){
var str = i.toString(r); if(str.length<r)str = "0"+str;
var ans = 0;
for(j=0;j<r;j++){
if(str.substr(j+1,r-j).match(str.charAt(j)))break;
else ans++;
}
if(ans==r){
document.write(math_plus(str));
for(j=0;j<r-1;j++){
document.write("a",(j+1),(eval(str.charAt(j))+1),"*");
}
document.writeln("a",r,(eval(str.charAt(r-1))+1));
}
}
先ほどのプログラムに追加。math_plus関数が目標とする関数だ。早速作ってみる。
math_plus = function(str){
var cnt = 0;
var pass_p = new Array();
var move = true;
for(k=0;k<str.length;k++)pass_p[k] = str.charAt(k);
while(move){
move = false;
for(l=0;l<str.length-1;l++){
var ex = [pass_p[l],pass_p[l+1]];
if(ex[0]>ex[1]){
pass_p[l] = ex[1];
pass_p[l+1] = ex[0];
cnt++;
move = true;
}
}
}
if(cnt%2==0)return "+";
else return "-";
}
これがそのプログラム。連続する2数を比べ、前者のほうが大きければ2数を入れ替えることによって配列をソートする。これをくわえてr=3を出力すると…
+a11*a22*a33 -a11*a23*a32 -a12*a21*a33 +a12*a23*a31 +a13*a21*a32 -a13*a22*a31
正しく符合がつけられている。これで行列の展開は成功だ。最後にこれらの関数を使いやすい形式にまとめておく。最初のa1やa2にはbが入ることもあるからだ。
math_plus = function(str){
var cnt = 0;
var pass_p = new Array();
var move = true;
for(k=0;k<str.length;k++)pass_p[k] = str.charAt(k);
while(move){
move = false;
for(l=0;l<str.length-1;l++){
var ex = [pass_p[l],pass_p[l+1]];
if(ex[0]>ex[1]){
pass_p[l] = ex[1];
pass_p[l+1] = ex[0];
cnt++;
move = true;
}
}
}
if(cnt%2==0)return "+";
else return "-";
}
open_square = function(r,b){
var clae = "";
for(i=Math.pow(r,r-2);i<Math.pow(r,r);i++){
var str = i.toString(r); if(str.length<r)str = "0"+str;
var ans = 0;
for(j=0;j<r;j++){
if(str.substr(j+1,r-j).match(str.charAt(j)))break;
else ans++;
}
if(ans==r){
clae+=math_plus(str);
for(j=0;j<r;j++){
if(eval(str.charAt(j))+1==b)clae+="b"+(j+1);
else clae+="a"+(j+1)+(eval(str.charAt(j))+1);
if(j!=r-1)clae+="*";
}
}
}
return clae;
}
rは元数、bはbの位置。0のときはbは入らない。ここまで準備があれば展開なんてたった数行。
open_square(3,0) open_square(3,1) open_square(3,2) open_square(3,3)
↓
+a11*a22*a33-a11*a23*a32-a12*a21*a33+a12*a23*a31+a13*a21*a32-a13*a22*a31 +b1*a22*a33-b1*a23*a32-a12*b2*a33+a12*a23*b3+a13*b2*a32-a13*a22*b3 +a11*b2*a33-a11*a23*b3-b1*a21*a33+b1*a23*a31+a13*a21*b3-a13*b2*a31 +a11*a22*b3-a11*b2*a32-a12*a21*b3+a12*b2*a31+b1*a21*a32-b1*a22*a31
一気に2,3,4の工程が終了した。(上)これらの式は最初のクラメル公式の各行列を展開したものなので、あとはクラメル公式通りにこれらの組み合わせを除算すれば連立方程式を解くことができる。
また、上の4個の計算結果のうち前半の処理は全て同じなのでさらに高速化ができる。(下)rを代入すると4つの式を全て生成する。
math_plus = function(str){
var cnt = 0;
var pass_p = new Array();
var move = true;
for(k=0;k<str.length;k++)pass_p[k] = str.charAt(k);
while(move){
move = false;
for(l=0;l<str.length-1;l++){
var ex = [pass_p[l],pass_p[l+1]];
if(ex[0]>ex[1]){
pass_p[l] = ex[1];
pass_p[l+1] = ex[0];
cnt++;
move = true;
}
}
}
if(cnt%2==0)return "+";
else return "-";
}
open_square_r = function(r){
var clae = new Array();
var clae_c = 0;
for(i=Math.pow(r,r-2);i<Math.pow(r,r);i++){
var str = i.toString(r); if(str.length<r)str = "0"+str;
var ans = 0;
for(j=0;j<r;j++){
if(str.substr(j+1,r-j).match(str.charAt(j)))break;
else ans++;
}
if(ans==r){
clae[clae_c] = new Array(math_plus(str),str);
clae_c++;
}
}
return clae;
}
open_square = function(r){
var claex = new Array();
var d = open_square_r(r);
for(i=0;i<=r;i++){
var b = i;
claex[i] = "";
for(j=0;j<d.length;j++){
claex[i]+= d[j][0];
var str = d[j][1];
for(k=0;k<r;k++){
if(eval(str.charAt(k))+1==b)claex[i]+="b"+(k+1);
else claex[i]+="a"+(k+1)+(eval(str.charAt(k))+1);
if(k!=r-1)claex[i]+="*";
}
}
}
return claex;
}
open_square(3) ↓ +a11*a22*a33-a11*a23*a32-a12*a21*a33+a12*a23*a31+a13*a21*a32-a13*a22*a31 +b1*a22*a33-b1*a23*a32-a12*b2*a33+a12*a23*b3+a13*b2*a32-a13*a22*b3 +a11*b2*a33-a11*a23*b3-b1*a21*a33+b1*a23*a31+a13*a21*b3-a13*b2*a31 +a11*a22*b3-a11*b2*a32-a12*a21*b3+a12*b2*a31+b1*a21*a32-b1*a22*a31
2005/10/09-2007/09/09
式ができてしまえばプログラム全体の9割が完成したも同然。残り1割を完成させた。n=7以上は時間がかかりすぎて危険。
(2007/09/09)圧倒的に高速化された連立方程式演算プログラム(3)が完成。