JavaScriptでマンデルブロー集合

マンデルブロー集合とは

2006/03/25

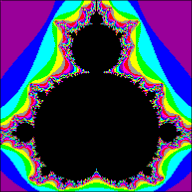
マンデルブロー集合とは複素数列Zが無限大に発散しないときの複素数Cの集合である。以下に示した画像はZ²を繰り返した標準的なマンデルブロー集合だ。画像の黒色の部分がマンデルブロー集合であり、その他の部分はZが発散する早さに応じて色をつけたものだ。

マンデルブロー集合の描き方

2006/03/25-2008/12/13

マンデルブロー集合は複素数の数列Zで定義される。Zの一般式は

$$Z_n={Z_{\mathrm{n-1}}}^p+C$$ $$C=a+bi$$ $$Z_0=0$$

で定義される。複素数Cをガウス平面上の1点(a,b)として、あるCを決めたときZ_nを計算し、その値の発散の有無を定めることでマンデルブロー集合を描く。Zにかかっている累乗pから分かるように、マンデルブロー集合はpの値によって形が変わる。

ここではp=2とした最も標準的なマンデルブロー集合を考える。複素数Zを

$$Z_n=X_n+Y_{n}i$$

として、数列に代入すると

$$X_n+Y_{n}i=\left({X_{\mathrm{n-1}}}^2-{Y_{\mathrm{n-1}}}^2+a\right)+\left(2X_{\mathrm{n-1}}{Y}_{\mathrm{n-1}}+b\right)i$$

即ち、実数と虚数の部分は

$$X_n={X_{\mathrm{n-1}}}^2-{Y_{\mathrm{n-1}}}^2+a$$ $$Y_n=2X_{\mathrm{n-1}}{Y}_{\mathrm{n-1}}+b$$

となる。

ガウス平面上(a,b)を定め、(X₀,Y₀)=(0,0)を初期値として上の式を適当な回数(nまで)反復計算し、Zの絶対値が定めた数値を超えるかどうかを判定する。通常、発散判定は次の式を用いる。

$$\sqrt{{X_n}^2+{Y_n}^2}>2$$

この発散判定は数列のどの部分で行っても良い。以上の結果をJavaScriptによって書き出す。ただし例では反復回数n=loopを50としている。

var k,x,y,zx,zy,a,b = 0;
var loop = 50;
for( k=0 ; k<loop ; k++ )
{
        zx = x*x-y*y+a;
        zy = 2*x*y+b;
        x = zx;
        y = zy;
        if( x*x+y*y>4 )break;
}

ループ計算を抜けたとき、変数kの値がloopと同じなら、収束しマンデルブロー集合であると見なし、未満なら発散したと見なす。最終的に集合を描くには、a,bの値を平面上の1点とし、ループ計算後のkの値に応じて色をつけていけばよい。

さらに実用的なプログラム(JavaScript)を書いておく。loopはループ(反復)回数、maxは計算範囲となる平面を何個に区切るか、PosXとPosYは計算する平面の中心座標、Zoomは倍率である。この設定だと中心座標を(0,0)とした2の範囲(-1〜1)を100マスに区切って計算し、2次の配列であるXtableに発散/収束時のループ回数kを代入する。

var a,b,x,y,zx,zy;
var Xtable = new Array();
var loop = 100;
var max = 100;
var med = max/2;
var PosX = 0;
var PosY = 0;
var Zoom = 2;
for( var i=0 ; i<max ; i++ )
{
        a = PosY + Zoom * ( (i-med) / max );
        Xtable[i] = new Array();
        for( var j=0 ; j<max ; j++ )
        {
                b = PosX + Zoom * ( (j-med) / max );
                x=0;y=0;
                for( var k=0 ; k<loop ; k++ )
                {
                        zx = x*x-y*y+a;
                        zy = 2*x*y+b;
                        x = zx;
                        y = zy;
                        if( x*x+y*y>4 )break;
                }
                Xtable[i][j] = k;
        }
}

後は座標(i,j)にXtable[i][j]の値によって分けた色をつけていくだけでマンデルブロー集合が描かれる。

JavaScriptでマンデルブロー

2006/03/25-2010/04/25

マンデルブロー集合は計算量が凄まじいので本来JSには不向きではあるが、JavaScriptで拡大可能なp=2〜6のマンデルブロー集合を実装。

(2010/04/25)動作確認はFirefox3.6,Opera10,GoogleChrome4,InternetExplorer8(何れもWindows)で動作確認済み、最速はOpera10,最も遅かったのはIE8。

マンデルブロー集合

拡大倍率

X4.00 X2.00 X1.00 X0.50 X0.25

解像度(2⁷*3)

32 48 64 96 128 192(危険) 384(危険)

ループ回数(高倍率時に精度を上げる)

64 125 216 512 729 1000 2197

カラーパレット

8色固定 ループ回数依存 同一色系統

状態

中心座標

倍率

倍

Debug(Cost)

ms

古いバージョン3:past3_mandel.js

古いバージョン2:past2_mandel.js

古いバージョン1:past1_mandel.js

ギャラリー

2006/03/25-2007/09/04

上のプログラムで描いたマンデルブロー集合の一片。何れも解像度は"危険"警告付の384*384。あの単純な収束式からは想像出来ない極めて複雑怪奇な紋様を作り出す。

• 8色固定版

ループ回数依存型のほうは現在作成中。